Set Operations

Set operations is a concept similar to fundamental operations on numbers. Sets in math deal with a finite collection of objects, be it numbers, alphabets, or any real-world objects. Sometimes a necessity arises wherein we need to establish the relationship between two or more sets. There comes the concept of set operations.

There are four main set operations which include set union, set intersection, set complement, and set difference.

What are Set Operations?

A set is defined as a collection of objects. Each object inside a set is called an ‘Element’. A set can be represented in three forms. They are statement form, roster form, and set builder notation. Set operations are the operations that are applied on two or more sets to develop a relationship between them. There are four main kinds of set operations which are as follows.

• Union of sets
• Intersection of sets
• Complement of a set
• Difference between sets/Relative Complement

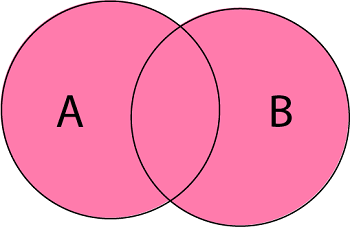
Before we move on to discuss the various set operations, let us recall the concept of Venn diagrams as it is important in understanding the operations on sets. A Venn diagram is a logical diagram that shows the possible relationship between different finite sets. The Venn diagram can be represented as follows.

Union of Sets

If two sets A and B are given, then the union of A and B is equal to the set that contains all the elements present in set A and set B. This operation can be represented as;

A ∪ B = {x: x ∈ A or x ∈ B}

Where x is the elements present in both sets A and B.

Example: If set A = {1,2,3,4} and B {6,7}

Solution:

A ∪ B = {1,2,3,4} ∪ {6,7}

A ∪ B = {1,2,3,4,6,7}

Then, Union of sets, A ∪ B = {1,2,3,4,6,7}

Example: Let A = {1, 2, 3} and B= {3, 4, 5, 6}

Solution:

A ∪ B = {1,2,3} ∪ {3, 4, 5, 6}

A ∪ B = {1, 2, 3, 4, 5, 6}.