A number or quantity that when multiplied with another number produces a given number or expression. For example, the factors of 12 are 1, 2, 3, 4, 6 and 12.
12 = 1 × 12
12 = 2 × 6
12 = 3 × 4
Any number can be expressed in the form of its factors as shown above.
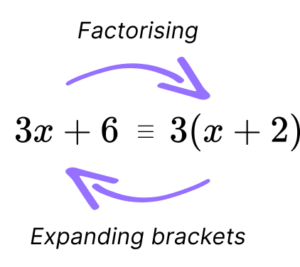
In terms of its prime factors, 12 can be expressed as:
12 = 2 × 3 × 2
Algebraic Expressions can be factorized using many methods. The most common methods used for factorization of algebraic expressions are:
- Factorization using common factors
- Factorization by regrouping terms
- Factorization using identities
Let us discuss these methods one by one in detail:
Factorization using common factors
To factorize an algebraic expression, the highest common factors of the terms of the given algebraic expression are determined and then we group the terms accordingly. In simple terms, the reverse process of expansion of an algebraic expression is its factorization.
To understand this more clearly let us take an example.
Example-
Solution:
The algebraic expression can be re-written as

Consider the algebraic expression 3y(- y + 6), if we expand this we will get -3y2 + 18y.
Factorization by regrouping terms
In some algebraic expressions, not every term may have a common factor. For instance, consider the algebraic expression 12a + n -na – 12. The terms of this expression do not have a particular factor in common but the first and last term has a common factor of ‘12’ similarly second and third term has n as a common factor. So the terms can be regrouped as:
⇒12a + n – na – 12= 12a – 12 + n – an
⇒12a – 12 – an + n = 12(a -1) –n(a -1)
After regrouping it can be seen that (a-1) is a common factor in each term,
⇒12a + n -na – 12=(a-1) (12 – n)
Thus, by regrouping terms we can factorize algebraic expressions.
Factorizing Expressions using standard identities
An equality relation which holds true for all the values of variables in mathematics is known as an identity. Consider the following identities:
On substituting any value of a and b, both sides of the given equations remain the same. Therefore, these equations are called identities.
Method 1 – Factoring Numbers and Basic Algebraic Expressions

Understand the definition of factoring when applied to single numbers.
Factoring is conceptually simple, but, in practice, can prove to be challenging when applied to complex equations. Because of this, it’s easiest to approach the concept of factoring by starting with simple numbers, then move on to simple equations before finally proceeding to more advanced applications. A given number’s factors are the numbers that multiply to give that number. For example, the factors of 12 are 1, 12, 2, 6, 3 and 4, because 1 × 12, 2 × 6, and 3 × 4 all equal 12.
- Another way to think of this is that a given number’s factors are the numbers by which it is evenly divisible.
- Can you find all the factors of the number 60? We use the number 60 for a wide variety of purposes (minutes in an hour, seconds in a minute, etc.) because it’s evenly divisible by a fairly wide range of numbers.
- The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.

Understand that variable expressions can also be factored.
Just as lone numbers can be factored, so too can variables with numeric coefficients be factored. To do this, simply find the factors of the variable’s coefficient. Knowing how to factor variables is useful for simplifying algebraic equations that the variables are a part of.[3]
- For example, the variable 12x can be written as a product of the factors of 12 and x. We can write 12x as 3(4x), 2(6x), etc., using whichever factors of 12 are best for our purposes.
- We can even go as far as to factor 12x multiple times. In other words, we don’t have to stop with 3(4x) or 2(6x) – we can factor 4x and 6x to give 3(2(2x) and 2(3(2x), respectively. Obviously, these two expressions are equal.

Apply the distributive property of multiplication to factor algebraic equations. Using your knowledge of how to factor both lone numbers and variables with coefficients, you can simplify simple algebraic equations by finding factors that the numbers and variables in an algebraic equation have in common. Usually, to make the equation as simple as possible, we try to search for the greatest common factor. This simplification process is possible because of the distributive property of multiplication, which states that for any numbers a, b, and c, a(b + c) = ab + ac.
- Let’s try an example problem. To factor the algebraic equation 12 x + 6, first, let’s try to find the greatest common factor of 12x and 6. 6 is the biggest number that divides evenly into both 12x and 6, so we can simplify the equation to 6(2x + 1).
- This process also applies to equations with negatives and fractions. x/2 + 4, for instance, can be simplified to 1/2(x + 8), and -7x + -21 can be factored to -7(x + 3).
Method 2 – Factoring Quadratic Equations

Ensure the equation is in quadratic form (ax2 + bx + c = 0).
Quadratic equations are of the form ax2 + bx + c = 0, where a, b, and c are numeric constants and a does not equal 0 (note that a can equal 1 or -1). If you have an equation containing one variable (x) that has one or more terms of x to the second power, you can usually shift the terms in the equation around using basic algebraic operations to get 0 on one side of equals sign and ax2, etc. on the other side.
- For example, let’s consider the algebraic equation. 5x2 + 7x – 9 = 4x2 + x – 18 can be simplified to x2 + 6x + 9 = 0, which is in the quadratic form.
- Equations with greater powers of x, like x3, x4, etc. can’t be quadratic equations. They are cubic equations, quartic equations, and so on, unless the equation can be simplified to eliminate these terms of x above the power of 2.

In quadratic equations where a = 1, factor to (x+d )(x+e), where d × e = c and d + e = b.
If your quadratic equation it is in the form x2 + bx + c = 0 (in other words, if the coefficient of the x2 term = 1), it’s possible (but not guaranteed) that a relatively simple shortcut can be used to factor the equation. Find two numbers that both multiply to make c and add to make b. Once you find these two numbers d and e, place them in the following expression: (x + d)(x + e). These two terms, when multiplied together, produce your quadratic equation – in other words, they are your quadratic equation’s factors.
- For example, let’s consider the quadratic equation x2 + 5x + 6 = 0. 3 and 2 multiply together to make 6 and also add up to make 5, so we can simplify this equation to (x + 3)(x + 2).
- Slight variations on this basic shortcut exist for slight variations in the equation itself:
- If the quadratic equation is in the form x2-bx+c, your answer is in this form: (x – _)(x – _).
- If it is in the form x2+bx+c, your answer looks like this: (x + _)(x + _).
- If it is in the form x2-bx-c, you answer is in the form (x + _)(x – _).
- Note: the numbers in the blanks can be fractions or decimals. For example, the equation x2 + (21/2)x + 5 = 0 factors to (x + 10)(x + 1/2).

If possible, factor by inspection.
Believe it or not, for uncomplicated quadratic equations, one of the accepted means of factoring is simply to examine the problem, then just consider possible answers until you find the right one. This is also known as factoring by inspection. If the equation is in the form ax2+bx+c and a>1, your factored answer will be in the form (dx +/- _)(ex +/- _), where d and e are nonzero numerical constants that multiply to make a. Either d or e (or both) can be the number 1, though this is not necessarily so. If both are 1, you’ve essentially used the shortcut described above.
- Let’s consider an example problem. 3x2 – 8x + 4 at first seems intimidating. However, once we realize that 3 only has two factors (3 and 1), it becomes easier, because we know that our answer must be in the form (3x +/- _)(x +/- _). In this case, adding a -2 to both blank spaces gives the correct answer. -2 × 3x = -6x and -2 × x = -2x. -6x and -2x add to -8x. -2 × -2 = 4, so we can see that the factored terms in parentheses multiply to become the original equation.

- For example, the equation x2 + 6x + 9 fits this form. 32 is 9 and 3 × 2 is 6. So, we know that the factored form of this equation is (x + 3)(x + 3), or (x + 3)2.

- Let’s return to the equation x2 + 5x + 6 = 0. This equation factored to (x + 3)(x + 2) = 0. If either of the factors equals 0, the entire equation equals 0, so our possible answers for x are the numbers that make (x + 3) and (x + 2) equal 0. These numbers are -3 and -2, respectively.

- Let’s plug -2 and -3 into x2 + 5x + 6 = 0. First, -2:
- (-2)2 + 5(-2) + 6 = 0
- 4 + -10 + 6 = 0
- 0 = 0. This is correct, so -2 is a valid answer.
- Now, let’s try -3:
- (-3)2 + 5(-3) + 6 = 0
- 9 + -15 + 6 = 0
- 0 = 0. This is also correct, so -3 is also a valid answer.
Method 3 – Factoring Other Forms of Equations

If the equation is in the form a2 – b2, factor it to (a + b)(a – b).
Equations with two variables factor differently than basic quadratics. For any equation a2 – b2 where a and b do not equal 0, the equation factors to (a + b)(a – b).
- For example, the equation 9x2 – 4y2 = (3x + 2y)(3x – 2y).

- The equation 4x2 + 8xy + 4y2 can be re-written as 4x2 + (2 × 2 × 2)xy + 4y2. We can now see that it’s in the correct form, so we can say with confidence that our equation factors to (2x + 2y)2

- For instance, 8x3 – 27y3 factors to (2x – 3y)(4x2 + ((2x)(3y)) + 9y2)