Profit

Profit in Maths is considered as the gain amount from any business activity. Whenever a shopkeeper sells a product, his motive is to gain some benefit from the buyer in the name of profit. Basically, when he sells the product more than its cost price, then he gets the profit on it but if he has to sell it for less than its cost price, then he has to suffer the loss.

The concept of profit and loss is basically defined in terms of business. Any financial benefit gained in business goes to the owner of the business.

In general, the profit is defined as the amount gained by selling a product, which should be more than the cost price of the product. It is the gain amount from any kind of business activity. In short, if the selling price (SP) of the product is more than the cost price (CP) of a product, then it is considered as a gain or profit. It describes the financial benefit obtained if the revenue from the business activity exceeds the taxes, expenses, and so on, which are involved in sustaining business activities.

Profit Formula

Profit is explained better in terms of cost price and selling price. Cost price is the actual price of the product or commodity and selling price is the amount at which the product is sold. So, if the selling price of the commodity is more than the cost price, then the business has gained its profit. Therefore formula to calculate the profit is;

Profit or Gain = Selling Price – Cost Price

But, when the product is sold at selling price lesser than the cost price, it is termed as loss. Therefore,

Loss = Cost Price – Selling Price

Profit Percentage

Once the profit is calculated we can also derive the percentage profit e have gained in any business by the formula given here;

P% = (P/CP) × 100

Where P is the profit and CP is the cost price

Types of Profit

There are three types of profit used in business. They are:

1. Gross Profit
2. Operating Profit
3. Net Profit

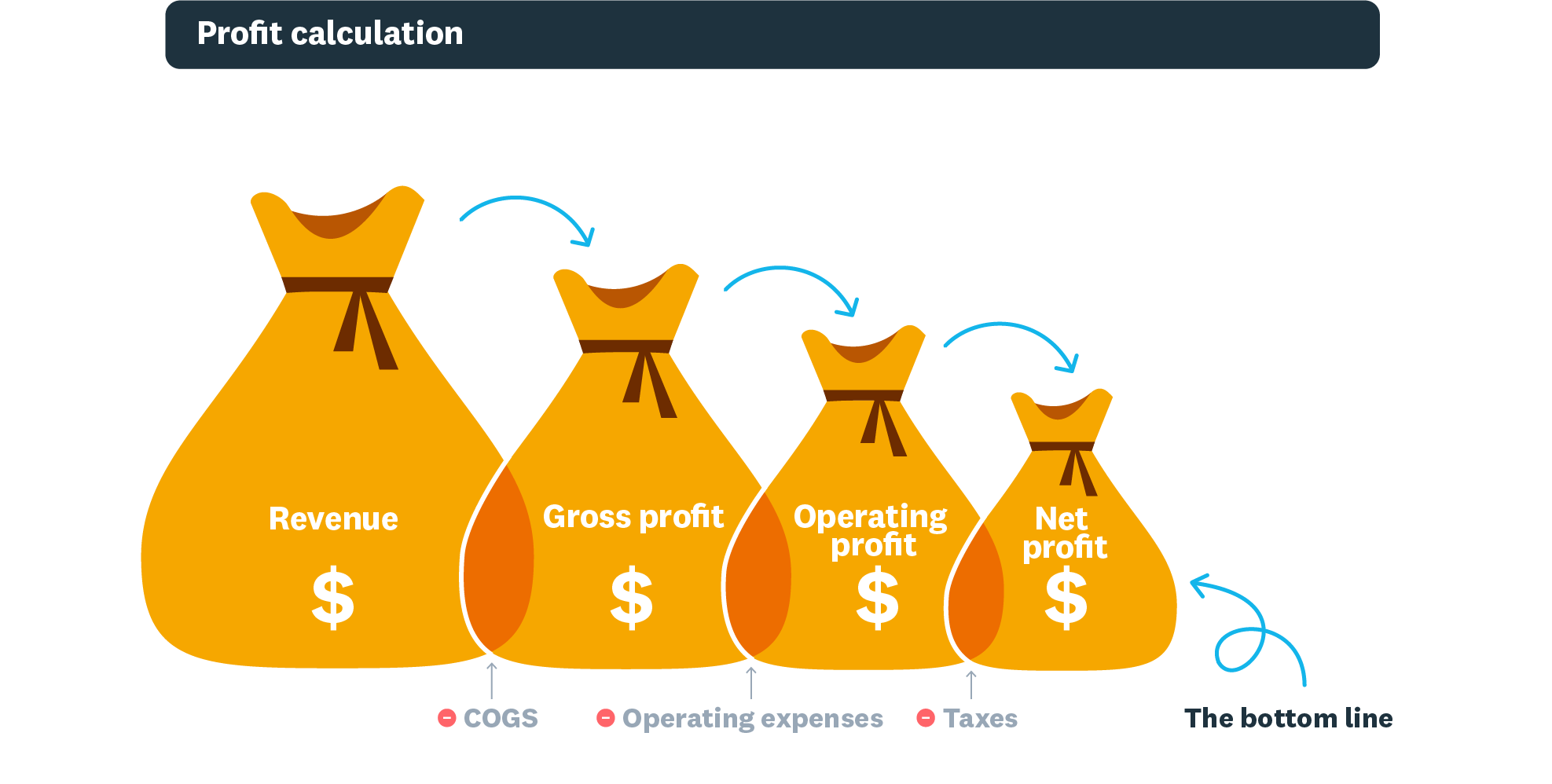
Gross Profit

Gross profit is the amount gained by any business or company after removing the cost associated with the making and selling of the product from the selling price. The revenue yielded in the company’s income after sales of the commodity should be reduced by the amount or cost it took to make the product or provide any service to the customer’s, to get the gross percentage of the profit.

The formula to calculate the Gross Profit is:

Gross Profit = Total Sales – COGs

Where COGs represents the cost of goods sold.

Operating Profit

A business’s operating profit tells what is the contribution of the company’s operations to its profitability. The operating profit is basically the ratio of operating income and sales revenue.

The formula to calculate the Operating Profit is:

Operating profit = Gross Profit – Operating Expenses

Also, Operating Profit Margin = Operating Profit / Total Sales

Net Profit

Net profit includes all the cost amount generated by the business as revenue. It represents the actual sum of money made by any business.

The formula to calculate the Net Profit is:

Net Profit = Operating Profit – (Taxes and Interest).

Companies examine all three types of profit with the help of a profit margin. In such case, the profit, whether gross, operating, or net, is divided by the return. It exhibits how well the business uses its earnings. A large ratio means it makes a lot of profit for each revenue. A low ratio means the business’s costs are consuming into its profits. Ratios vary according to each trade.

How to Calculate Profit?

To calculate the profit gained by any business, follow the steps below:

• Determine the cost price of the products sold.
• Now calculate the total selling price of the products sold.
• Subtract the cost price and selling price, to get the profit amount.
• To calculate the profit margin, divide the profit amount with cost price.
• Multiply the profit margin with 100 to get in percentage.

Example:  If a shopkeeper sells Apple at Rs.200 per kg, whose cost price is Rs.150/- per kg. Then find the profit gained by the shopkeeper.

Solution: 

Given Cost Price = Rs.150/-

And Selling Price = Rs.200/-

From the formula of profit, we know,

Profit = Selling Price – Cost Price

P = 200 – 150

P = 50

Therefore, the shopkeeper gains Rs.50/- from the business.

Example: Salman sold a digital camera for Rs.5,000, on which he gains 25%. What is the cost price of the camera?

Solution:

For the digital camera: Gain = 25%.

Let cost price (C.P.) = Rs.100.

Therefore, selling price (S.P.) = (100 + 25) = 125

When selling price (S.P.) is Rs.125, cost price (C.P.) is Rs.100.

Therefore, when selling price (S.P.) is Rs.5000,

cost price (C.P.) = 100/125 × 5000 = (100 × 5000)/125 = 500000/125 = 4000

Therefore, cost price (C.P.) of the digital camera = Rs. 4000.

Example: A shopkeeper buys watches in bulk for Rs. 20 each. He sells them for Rs. 45 each. Calculate the profit and the profit percentage.

Solution:

Given,

Selling price of the watch = Rs. 45

Cost price of the watch = Rs. 20

Now, Profit = Selling Price – Cost Price

So, profit on the watch = 45 – 20 = Rs. 25

Using the formula for profit percentage,

Profit % = (Profit / C.P.) × 100

So, the profit percentage of the shopkeeper will be (25 / 20) × 100 = 1.25 × 100 = 125%.

It can be said that the shopkeeper made a profit of Rs. 25 from each watch with a profit percentage of 125%.

Mark up

Mark up refers to the value that a player adds to the cost price of a product. The value added is called the mark-up. The mark-up added to the cost price usually equals retail price.

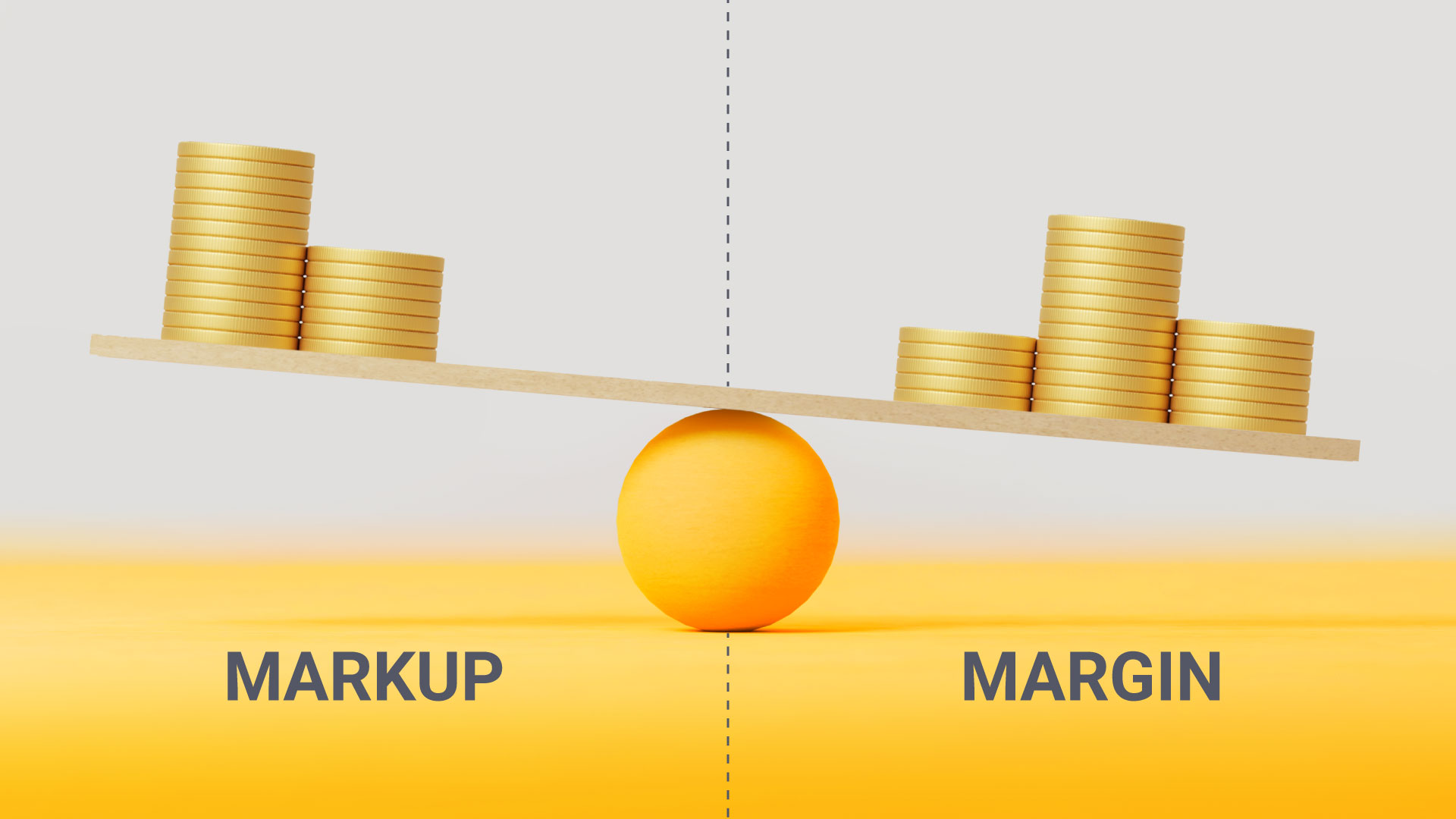
Markup =Gross Profit / Cost Price

Margin = Gross Profit / Selling Price

What’s the Difference Between Markup and Profit?

A retail farm market manager knows that their business needs to make a certain gross profit percentage, in this case, let’s say 30%. What do they do? The manager takes the cost of the item and adds 30%. Does adding 30% markup to that item really mean you are making a 30% profit? 

Well, no. To determine the profit you made on an item, you need to take the markup amount and divide that by the sale price of the item and that will give you your profit margin.

Here’s an example. Let’s say an item in your store cost you $1.00 to purchase. You take that item and add 30% to it. Now, you sell the item for $1.30. You’ve made .30 cents on that item. You divide .30 by 1.30 and you will see you’ve made only 23% gross profit on that item. Think about every item in your market. If you were adding 30% to all your products and thinking you are making a 30% gross profit margin when in fact you are losing almost ¼ of your gross profits.

If we go back to $1.00 product cost, that product would need to sell for $1.44 to make a 30% profit on it. Again, take .44 (the profit made from the item) and divide it by the sale price of $1.44 and you get a 30% profit margin.

Figuring out your markup percentage

The markup percentage is your unit cost X the markup percentage, and then add that to the unit cost to get your sales price.

For example, if the unit cost is $5.00, the selling price with a 30% markup would be $6.50:

• Gross Profit Margin = Sales Price – Unit Cost = $6.50 – $5.00 = $1.50.

• Markup Percentage = Gross Profit Margin/Unit Cost = $1.50/$5.00 = 30%.

• Sales Price = Cost X Markup Percentage + Cost = $5.00 X 30% + $5.00 = $6.50.

How to calculate gross profit margin percentage?

Gross profit margin defined is Gross Profit divided by Sales Price. In this example, the gross profit margin is $1.50. This gives us a 23% gross profit margin percentage:

Gross Profit Margin Percentage = Gross Profit/Sales Price 

Gross Profit Margin Percentage =  $1.50/$6.50 = 23%.

These are rather simplified examples and we don’t have the same profit expectations for every item in our market. However, if we understand the difference between markup percentages and gross profit margins, we can have better flexibility in our pricing strategies.

Our customers have certain expectations on the price of our fruits and vegetables so we may not have that much flexibility on what we can charge but if we can create packages or bundles with value added items that we can have a higher gross profit margin on, we can thereby increase the overall gross profit for that fruit or vegetable.