Angle 

An angle is formed when two lines intersect each other. We represent an angle by the symbol ∠.

An angle involves two legs and one common vertex at which two lines meet.

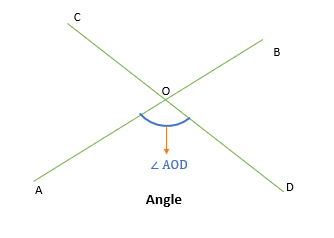
For example, ∠AOD is formed when lines AB and CD intersect with each other.

Also, ∠AOD is formed between the leg AO and OD, so we include A, O, and D while naming the angle.

Do you know that the position of leg points does not matter as long as the common vertex is the middle letter in the angle name?

Measurement of an Angle

The angle is measured in degrees.

An angle can measure from zero (0) degrees to 360 degrees. Based on the measurement of an angle, they are divided into four types:

1. Acute angle
2. Right angle
3. Obtuse angle
4. Reflex angle

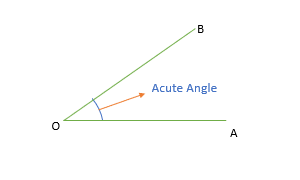
Acute Angle

When the measurement of the angle is between 0 degrees and 90 degrees.

Right Angle

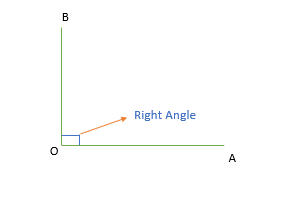
When the measurement of the angle is exactly 90 degree.

• If there is a right angle between two lines, then the two lines are said to be perpendicular to each other.

Obtuse Angle

When the measurement of the angle is between 90 degrees and 180 degrees.

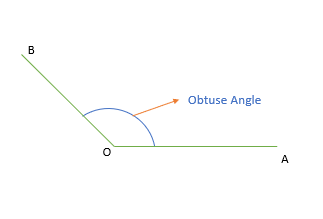
A straight line has an angle of 180 degrees.

Reflex Angle

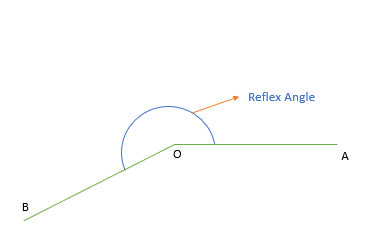
When the measurement of the angle is between 180 degrees and 360 degrees.

Complementary Angles

Complementary Angles are those which add together to make 90°.

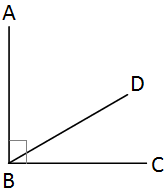
The examples above all show two angles that are complementary. Notice that the angles do not have to be adjacent to be complementary. If they are adjacent then they form a right angle.

Supplementary Angles

Supplementary Angles add together to make 180°

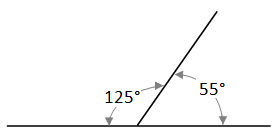
The two angles shown above are supplementary to each other. They add together to give 180°. They can be said supplement each other. Note that, as with complementary angles, they do not need to be adjacent to each other.

Opposite Angles

When to lines intersect they create four angles. Each angle is opposite to another and form a pair of what are called opposite angles.

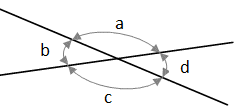
Opposite angles are sometimes called vertical angles or vertically opposite angles.

Example:

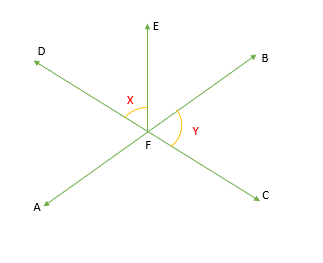
1. In the diagram given above, angle DFE and angle BFC are represented by X and Y respectively. If ∠AFC = 100° and ∠BFE = 45°then what is the value of Y-X?

Solution

Step 1: Given

• ∠DFE = X
• ∠BFC = Y
• ∠AFC = 100°
• ∠BFE = 45°

Step 2: To find

• The value of Y-X

Step 3: Approach and Working out

To find Y-X, we need to find Y and X first.

Measure of angle Y:

• We are given ∠AFC = 100° and,
  • ∠AFC + ∠BFC = 180° as the sum of angles on the same side straight line is 180°
  • 100° + ∠BFC = 180°
    • ∠BFC = Y = 80°

Measure of angle X:

• We are given ∠BFE = 45° and,
  • ∠DFE + ∠BFE + ∠BFC = 180° as the sum of angles on the same side straight line is 180°.
  • X + 45° +80°= 180°
    • X = 55°

Hence, Y – X = 80° – 55° =25°.

2. An angle measures 40°. Find its supplement and complement.

Solution: