What Are Algebraic formulas ?
Algebraic formulas are equations in algebra where the value of the left-hand side of the equation is identically equal to the value of the right-hand side of the equation. They are satisfied with any values of the variables. Let us consider an example to understand this better.
Consider the equations: 5x – 3 = 12, 10x – 6 = 24, and x2 + 5x + 6 = 0. These equations satisfy only for certain value(s) of x and do not work for any value in general.
Now let us consider an equation x2 – 9 = (x + 3)(x – 3).
Note that this equation is satisfied for any value of x (try to substitute any number for x on both left and right sides, you should be getting the same answer).
These are helpful to work out numerous math problems. The four basic algebra identities are as follows.
Identity-I: (a + b)2 = a2 + 2ab + b2
Identity-II: (a – b)2 = a2 – 2ab + b2
Identity-III: (a + b)(a – b) = a2 – b2
Identity-IV: (x + a)(x + b) = x2 + (a + b) x + ab
Verify: (a + b)2 = a2 + 2ab + b2
Algebraic Verification:
(a + b)2 = a2 + b2
Step 1: Given data
We have to prove the identity-
(a + b)2 = a2 + 2ab + b2
Step 2: Proving the identity
L.H.S = (a + b)2 = (a + b)(a + b)
a(a + b) + b(a + b) = a² + ab + ab + b² = a² + 2ab + b² = R.H.S
L.H.S = R.H.S
Therefore, the algebraic identity (a + b)² = a² + 2ab + b² is verified
Geometrical Verification:
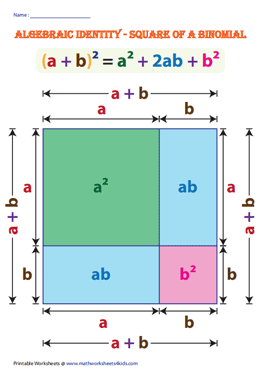
Examples:
Using the identity , simplify
Given –
Using this Identity,
=
=
Using the identity , simplify
As We Know from the question, substituting the values
we Get,
=
Evaluate by using the identity
Using =
We can write
=
Hence the answer is
Verify: (a – b)2 = a2 – 2ab + b2
Algebraic Verification:
(a – b)2 = a2 – b2
Step 1: Given data
We have to prove the identity-
(a – b)2 = a2 – 2ab + b2
Step 2: Proving the identity
L.H.S = (a – b)2 = (a – b)(a – b)
a(a – b) – b(a – b) = a² – ab – ab + b² = a² – 2ab + b² = R.H.S
L.H.S = R.H.S
Therefore, the algebraic identity (a – b)² = a² – 2ab – b² is verified
Geometrical Verification:
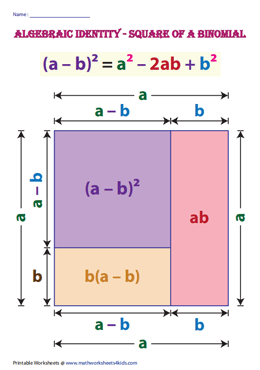
Examples:
Find the value of (x – 2y)2 by using the (a – b)2 formula.
Solution:
To find: The value of (x – 2y)2.
Let us assume that a = x and b = 2y.
We will substitute these values in (a – b)2 formula:
(a – b)2 = a2 – 2ab + b2
(x-2y)2 = (x)2 – 2(x)(2y) + (2y)2
= x2 – 4xy + 4y2
(x – 2y)2 = x2 – 4xy + 4y2
Factorize x2 – 6xy + 9y2 by using a minus b Whole Square Formula.
Solution:
To factorize: x2 – 6xy + 9y2.
We can write the given expression as:
x2 – 6xy + 9y2 = (x)2 – 2 (x) (3y) + (3y)2.
Using (a – b)2 formula:
a2 – 2ab + b2 = (a – b)2
Substitute a = x and b = 3y in this formula:
(x)2 – 2 (x) (3y) + (3y)2 = (x – 3y)2
x2 – 6xy + 9y2 = (x – 3y)2
Simplify the following using (a – b)2 formula.
(7x – 4y)2
Solution:
a = 7x and b = 4y
Using formula (a – b)2 = a2 – 2ab + b2
(7x)2 – 2(7x)(4y) + (4y)2
49x2 – 56xy + 16y2
(7x – 4y)2 = 49x2 – 56xy + 16y2.
Verify: (a + b)(a – b) = a2 – b2
Algebraic Verification:
(a + b)(a – b) = a2 – b2
Step 1: Given data
We have to prove the identity-
(a + b)(a – b) = a2 – b2
Step 2: Proving the identity
L.H.S = (a + b)(a – b)
Expanding the terms, we get
= a(a – b) + b(a – b)
= a² – ab + ab – b²
= a2 + 0 + b2
= a2 – b2 = R.H.S
L.H.S = R.H.S
Therefore, the algebraic identity (a + b)(a – b) = a2 – b2 is verified
Geometrical Verification:
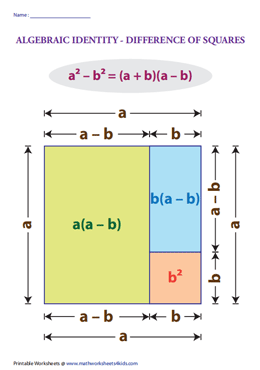
Examples:
Using a2 – b2 formula find the value of 1062 – 62.
Solution:
To find: 1002 – 62.
Let us assume that a = 100 and b = 6.
We will substitute these in the a2 – b2 formula.
a2 – b2 = (a – b) (a + b)
1062 – 62 = (106 – 6) (106 + 6)
= (100) (112)
= 11200
1062 – 62 = 11200.
Factorize the expression 25x2 – 64.
Solution:
To factorize: 25x2 – 64.
We will use the a2 – b2 formula to factorize this.
We can write the given expression as
25x2 – 64 = (5x)2 – 82
We will substitute a = 5x and b = 8 in the formula of a2 – b2.
a2 – b2 = (a – b) (a + b)
(5x)2 – 82 = (5x – 8) (5x + 8)
25x2 – 64 = (5x – 8) (5x + 8)
Simplify 102 – 52 using a2 – b2 formula
Solution:
To find 102 – 52
Let us assume a = 10 and b = 5
Using formula a2 – b2 = (a – b) (a + b)
102-52 = (10 – 5) (10 + 5)
= 10(10 +5) – 5(10 + 5)
= 10(15) – 5(15)
= 150-75 = 75
102 – 52 = 75.
Verify: (x + a)(x + b) = x2 + (a + b) x + ab
Algebraic Verification:
(x + a)(x + b) = x2 + (a + b) x + ab
Step 1: Given data
We have to prove the identity-
(x + a)(x + b) = x2 + (a + b) x + ab
Step 2: Proving the identity
L.H.S = (x + a)(x + b)
Expanding the terms, we get
= x(x + b) + a(x + b)
= x² + bx + ax + ab
Taking x common from ax and bx
= x² + (a + b) x + ab = R.H.S
L.H.S = R.H.S
Therefore, the algebraic identity (x + a)(x + b) = x2 + (a + b) x + ab is verified
Geometrical Verification:
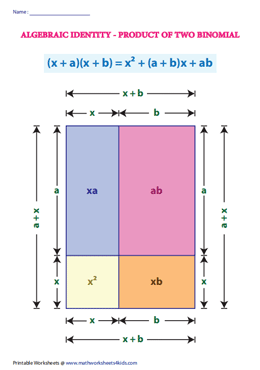
Examples:
Use the identity (x + a)(x + b) = x2 + (a + b)x + ab to find the following products
(i) (x + 3)(x + 7)
(x + 3)(x + 7)
= x2 + (3 + 7)x + (3)(7)
= x2 + 10x + 21
(ii) (4x + 5)(4x + 1)
(4x + 5)(4x + 1)
= (4x)2 + (5 + 1)(4x) + (5)(1)
= 16x2 + 24x + 5
(iii) (4x – 5)(4x -1)
(4x – 5)(4x – 1)
= (4x)2 + [(-5) + (-1)](4x) + (-5) (-1)
= 16x2 – 24x + 5
(iv) (4x + 5)(4x -1)
(4x + 5)(4x -1)
= (4x)2 + [(5) + (-1)](4x) + (5)(-1)
= 16x2 + 16x – 5
(v) (2x + 5y)(2x + 3y)
(2x + 5y)(2x + 3y)
= (2x)2 + (5y + 3y)(2x) + (5y)(3y)
= 4x2 + 16xy + 15y2
(vi) (2a2 + 9)(2a2 + 5)
(2a2 + 9)(2a2 + 5)
= (2a2)2 + (9 + 5)(2a2) + (9)(5)
= 4a4 + 28a2 + 45