Commutative Law of Sets

Sets are the collection of elements or objects. In sets, we have learned about different types of operations performed on them such as intersection of sets, union of sets, difference of sets, etc.

According to the Commutative law for Union of sets and the Commutative law for Intersection of sets, the order of the sets in which the operations are done, does not change the result.

So, if A and B are two different sets, then, as per commutative law;

A ∪ B = B ∪ A  [Union of sets]

A ∩  B = B ∩ A   [Intersection of sets]

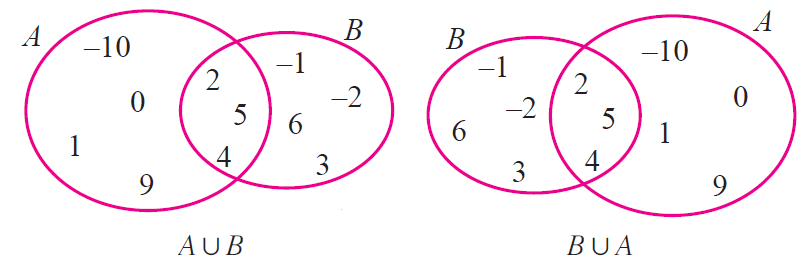
For example, if A = {1, 2, 3} and B = {3, 4, 5, 6}, then;

A Union B = A ∪ B = {1, 2, 3, 4, 5, 6}  …….. (i)

B Union A = B ∪ A = {1, 2, 3, 4, 5, 6}   ……… (ii)

From (i) and (ii), we get;

A ∪ B = B ∪ A

Now, 

A intersection B = A ∩ B = {3}   ……..(iii)

B intersection A = B ∩ A = {3}   ……..(iv)

From (iii) and (iv), we get;

A ∩ B = B ∩ A

Hence, proved commutative law for union and intersection of two sets.

Examples

1. Verify the commutative property of union and intersection of sets for the following.
A = {l, m, n, o, p, q}  B = {m, n, o, r, s, t}