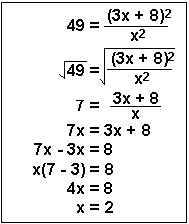Manipulation of Algebraic Expression

Algebraic manipulation refers to the manipulation of algebraic expressions, often into a simpler form or a form which is more easily handled and dealt with. The skill of algebraic manipulation is acquired through practice and solving problems.

Algebraic manipulation involves doing opposite operations (undoing) to any equation to solve for a certain variable (often by isolation).

Properties of Equality

Any time we add, subtract, multiply, divide, square, square root, etc. to one side, we must do it to the other side to maintain equality.

Example

$\begin{align*} x^2 + 18 &= 43 \\ x^2 &= 25 \\ x &= \boxed{\pm 5} \end{align*}$

In the example, we first subtract 18 from the left side to isolate the $x^2$ . However, we also have to subtract 18 from the right side to maintain equality. The right hand side becomes $43 - 18 = 25$ .

We then square root the left side to get the $x$ by itself. However, we also have to square root the right side to maintain equality.

Cross Multiplication

Cross multiplication is a common method of solving proportions. Essentially, one is multiplying both sides by the denominators of both sides.

Example

$\begin{align*} \frac{x}{3} &= \frac{10}{5} \\ 5 \cdot x &= 3 \cdot 10 \\ 5x &= 30 \\ x &= 6 \end{align*}$

The above method of solving is an example of cross-multiplication. During the cross-multiplication, we actually multiplied both sides by $3 \cdot 5$ . On the LHS, the $3$ gets divided out (leaving a $5$ for multiplication), and on the RHS, the $5$ gets divided out (leaving a $3$ for multiplication).

Potential Extraneous Solutions

In some methods of isolation like squaring both sides or multiplying both sides by a non-constant, we could introduce additional “solutions” that aren’t really solutions to the original equation. Such solutions are called “extraneous solutions”. Thus, when doing such methods, it is a good idea to check the solutions by plugging it back into the original equation.

Additionally, when dividing both sides by a non-constant, we could eliminate perfectly valid solutions. Thus, when possible, it’s often better to factor than to divide both sides.

Example

$\begin{align*} \frac{x^2 - 2x}{x-5} &= \frac{15}{x-5} \\ x^2 - 2x &= 15 \\ x^2 - 2x - 15 &= 0 \\ (x-5)(x+3) &= 0 \\ x &= 5, -3 \end{align*}$

When solving, we start by multiplying both sides by $x-5$ . Then we used algebraic manipulation to get all terms to one side to form a quadratic. After factoring, we get $x = 5, -3$ .

Plugging in $x = -3$ satisfies the original equation because $\frac{9+6}{-8} = \frac{15}{-8}$ . However, plugging in $x = 5$ does not satisfy the original equation because $\frac{15}{0}$ on both sides is undefined. Thus, $x = -3$ is the only valid solution, and $x = 5$ is an extraneous solution.

The extraneous solution appeared when we multiplied both sides by $x - 5$ . The original equation banned $x = 5$ as a possible solution because it would make the denominator zero. However, after multiplying both sides by $x-5$ , there is no denominator that eliminates $x = 5$ as a possible solution.

The key to solving simple algebraic equations containing a single unknown (e.g. x + 6 = 10) is to realize that the equation is an equality. As long as you do the same mathematical operation (e.g. add a constant, subtract a constant, multiply by a constant, and divide by a constant) to both sides of the equation, the equality is still an equality. This includes squaring both sides of the equation or taking the square root of both sides of the equation.

Fundamental Laws:

Distributive Law: 3(x + 2) = 3x + (3)(2) = 3x + 6
Associative Law: 4x – 7x = x(4 – 7) = -3x

Examples

1. To solve for x, it is necessary to subtract 6 from both sides of the equation

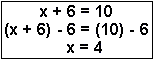
2. To solve for x, you need to add 6 to both sides of the equation and then divide both sides by 2.

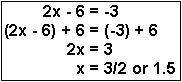
3. To isolate x, you need to

multiply through by 6,
subtract 2 from both sides, and
divide both sides by 5.

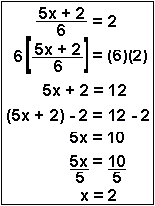
4. To solve for x this time, you need to

multiply both sides of the equation by 4 and 3 to cancel out the denominator in line 2,
use the distributive law,
by adding and subtracting, move the x terms to one side, and the non-x terms to the other side in line 5,
use the associative law to simplify to get line 7, and
divide both sides by 2.

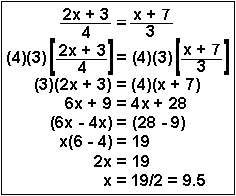
Alternative Method

This process is called “cross-multiplying.” This entails multiplying the numerator of one side of the equality by the denominator of the other side of the equality. When this is done, the very same line 3 results. The rest of the problem is done identically.

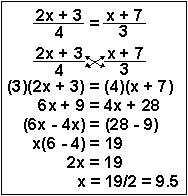
5. This problem could be very complicated and become a quadratic equation. However, because it has a perfect square on both sides, if you simply take the square root of both sides of the equality, you are left in line 3 with a straightforward algebra problem as you solve for the positive root, which I did here.

In Chemistry, when we use this technique to solve equilibrium problems, only one of the roots is meaningful. Of course, the square root of 49 can be -7 as well as +7. You can then go ahead and solve for the second root, x = -0.8 = -4/5.