The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”.
A polynomial can have any number of terms but not infinite.
Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates.
We can perform arithmetic operations such as addition, subtraction, multiplication and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x2+x-12. In this example, there are three terms: x2, x and -12.
The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial can have any number of terms but not infinite.
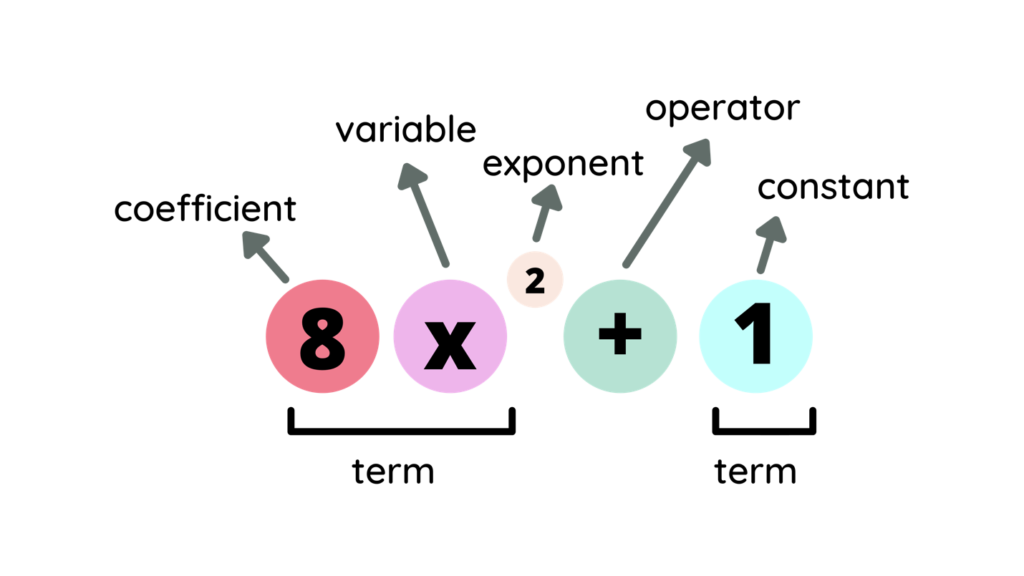
What is a Polynomial?
A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using the mathematical operations such as addition, subtraction, multiplication and division (No division operation by a variable).
Based on the numbers of terms present in the expression, it is classified as monomial, binomial, and trinomial. Examples of constants, variables and exponents are as follows:
- Constants. Example: 1, 2, 3, etc.
- Variables. Example: g, h, x, y, etc.
- Exponents: Example: 5 in x5 etc.
Polynomial Examples
Let us understand this by taking an example: 3x2 + 5. In the given polynomial, there are certain terms that we need to understand.
Here, x is known as the variable. 3 which is multiplied to x2 has a special name. We denote it by the term “coefficient”. 5 is known as the constant. The power of the variable x is 2.
Below given are a few expressions that are not examples of a polynomial.
| Not a Polynomial | Reason |
|---|---|
| 2x-2 | Here, the exponent of variable ‘x’ is -2. |
| 1/(y + 2) | This is not an example of a polynomial since division operation in a polynomial cannot be performed by a variable. |
| √(2x) | The exponent cannot be a fraction (here, 1/2) for a polynomial. |
Notation
The polynomial function is denoted by P(x) where x represents the variable. For example,
P(x) = x2-5x+11
If the variable is denoted by a, then the function will be P(a)
Degree of a Polynomial
The degree of a polynomial is defined as the highest degree of a monomial within a polynomial. Thus, a polynomial equation having one variable which has the largest exponent is called a degree of the polynomial.
| Polynomial | Degree | Example |
|---|---|---|
| Constant or Zero Polynomial | 0 | 6 |
| Linear Polynomial | 1 | 3x+1 |
| Quadratic Polynomial | 2 | 4x2+1x+1 |
| Cubic Polynomial | 3 | 6x3+4x3+3x+1 |
| Quartic Polynomial | 4 | 6x4+3x3+3x2+2x+1 |
Example: Find the degree of the polynomial 6s4+ 3x2+ 5x +19
Solution:
The degree of the polynomial is 4.
Terms of a Polynomial
The terms of polynomials are the parts of the equation which are generally separated by “+” or “-” signs. So, each part of a polynomial in an equation is a term.
For example, in a polynomial, say, 2x2 + 5 +4, the number of terms will be 3. The classification of a polynomial is done based on the number of terms in it.
| Polynomial | Terms | Degree |
| P(x) = x3-2x2+3x+4 | x3, -2x2, 3x and 4 | 3 |
Like Terms and Unlike Terms
Like terms in polynomials are those terms which have the same variable and same power. Terms that have different variables and/or different powers are known as unlike terms.
Hence, if a polynomial has two variables, then all the same powers of any ONE variable will be known as like terms. Let us understand these two with the help of examples given below.
For example, 2x and 3x are like terms. Whereas, 3y4 and 2x3 are unlike terms.
Types of Polynomials
Polynomials can be categorized based on their degree and their power. Based on the numbers of terms, there are mainly three types of polynomials that are listed below:
- Monomials
- Binomials
- Trinomials
Monomial
A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:
- 5x
- 3
- 6a4
- -3xy
Binomial
A binomial is a polynomial expression which contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:
- – 5x+3,
- 6a4 + 17x
- xy2+xy
Trinomial
A trinomial is an expression which is composed of exactly three terms. A few examples of trinomial expressions are:
- – 8a4+2x+7
- 4x2 + 9x + 7
