Pythagorean Theorem 

The Pythagorean Theorem, also referred to as the ‘Pythagoras theorem,’ is arguably the most famous formula in mathematics that defines the relationships between the sides of a right triangle.

The theorem is attributed to a Greek mathematician and philosopher named Pythagoras (569-500 B.C.E.). He has many contributions to mathematics, but the Pythagorean Theorem is the most important of them.

What is the Pythagorean Theorem?

The Pythagoras theorem is a mathematical law that states that:

“The sum of squares of the lengths of the two short sides of the right triangle is equal to the square of the length of the hypotenuse.”

Pythagoras Theorem Equation

The Pythagoras theorem equation is expressed as,

 where ‘c’ = hypotenuse of the right triangle and ‘a’ and ‘b’ are the other two legs. Hence, any triangle with one angle equal to 90 degrees produces a Pythagoras triangle and the Pythagoras equation can be applied in the triangle.

There are many demonstrations of the Pythagorean Theorem given by different mathematicians.

Another common demonstration is to draw the 3 squares in such a way that they form a right triangle in between, and the area of the bigger square (the one at hypotenuse) is equal to the sum of the area of the smaller two squares (the ones on the two sides).

Consider the 3 squares below:

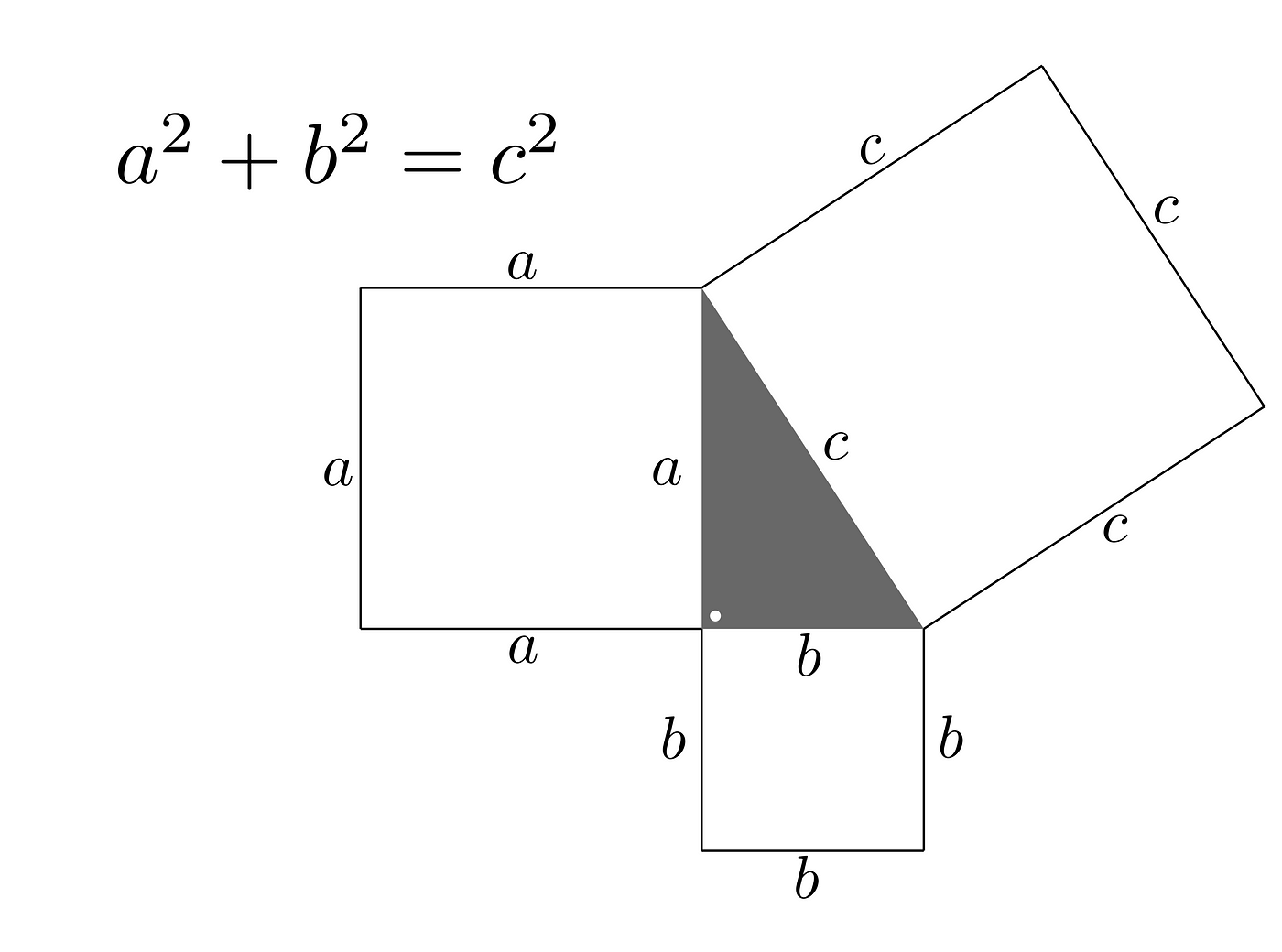
It is one of these primaries theorem of all science. Just to say about vector notation as being involved in everything. Classical mechanics, electromagnetism, relativity, quantum mechanics are all benefits. If that so, it is good to not only know how to use it but also why it holds.

For that purpose, assume we have a sector divided at any point into two smaller pieces, called a and b, which are catheti of a right triangle.

Next, we need to add the hypotenuse, but to draw it, we have to move into 2D. So we treat the sector a+b as the length of the side of a square.

We additionally know that the area of a square is its side times side. In our case:

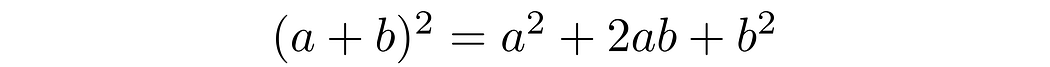
Now let’s form our triangle by cutting this area into smaller parts as follows:

What we got are four identical right triangles of sides: a, b, c, and one square, which has side c. Their total area is equal to:

We fulfill the whole area of the initial square while forming them; thereby their total area has to be equal to the area of the square.

Let’s see if it really works using an example.

Example:

A “3, 4, 5” triangle has a right angle in it.

Let’s check if the areas are the same: 32 + 42 = 52 Calculating this becomes: 9 + 16 = 25 It works … like Magic!

Applications of Pythagoras Theorem

• To know if the triangle is a right-angled triangle or not.
• In a right-angled triangle, we can calculate the length of any side if the other two sides are given.
• To find the diagonal of a square.

Why Is This Useful?

If we know the lengths of two sides of a right-angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!)