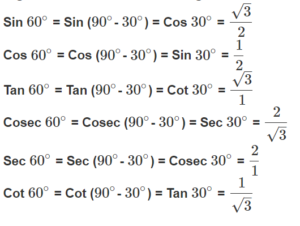Course Content
Chapter 01 – Operations on Sets
The set operations are performed on two or more sets to obtain a combination of elements as per the operation performed on them. In a set theory, there are three major types of operations performed on sets, such as: Union of sets (∪) The intersection of sets (∩) Difference of sets ( – ) In this lesson we will discuss these operations along with their Venn diagram and will learn to verify the following laws: Commutative, Associative, Distributive, and De-Morgans' law.
0/14
Subsets and Super Sets
03:10
Venn Diagrams
03:32
Operations on Set
00:00
Union of Sets
06:11
Intersection of Sets
06:13
Difference of Sets
05:15
Complement of Sets
06:21
Let's Try
Venn Diagrams (Three or More Sets)
03:21
Let's Try
Commutative Law of Union and Intersection
02:53
Associative Law of Union and Intersection
05:01
Distributive Law over Union and Intersection
04:13
De Morgan’s Law
05:25
Chapter 02 – Real Numbers
All real numbers follow three main rules: they can be measured, valued, and manipulated. Learn about various types of real numbers, like whole numbers, rational numbers, and irrational numbers, and explore their properties. In this chapter, we will learn about Squares and cubes of real numbers and find their roots.
0/6
Irrational Numbers
05:54
Squares
03:04
Square Roots
03:49
Let's Try
Cubes and Cube Roots
11:23
Let's Try
Chapter 03 – Number System
The number system or the numeral system is the system of naming or representing numbers. There are different types of number systems in Mathematics like decimal number system, binary number system, octal number system, and hexadecimal number system. In this chapter, we will learn different types and conversion procedures with many number systems.
0/13
Number System
08:13
Conversion – Base 2
00:00
Addition in Binary System
03:02
Subtraction in Binary System
02:32
Multiplication in Binary System
02:43
Conversion – Base 5
00:00
Addition in Base 5
01:55
Subtraction in Base 5
01:38
Multiplication in Base 5
04:17
Conversion – Base 8
08:19
Addition & Subtraction in Base 8
06:07
Multiplication in Base 8
04:39
Let's Try
Chapter 04 – Financial Arithmetic
Financial mathematics describes the application of mathematics and mathematical modeling to solve financial problems. In this chapter, we will learn about partnership, banking, conversion of currencies, profit/markup, percentage, and income tax.
0/11
Compound Proportion
05:10
Partnership
07:17
Inheritance
09:53
Conversion of Currencies
03:13
Profit or Markup
07:00
Percentage
08:30
Let's Try
Taxes
03:46
Income Tax
02:15
Let's Try
Banking
06:16
Chapter 05 – Polynomials
In algebra, a polynomial equation contains coefficients, exponents, and variables. Learn about forming polynomial equations. In this chapter, we will study the definition and the three restrictions of polynomials, we'll tackle polynomial equations and learn to perform operations on polynomials, and learn to avoid common mistakes.
0/6
Algebraic Expression
02:38
Polynomials
08:19
Addition and Subtraction of Polynomial
15:05
Multiplication of Polynomials
02:42
Division of Polynomial
10:49
Let's Try
Chapter 06 – Factorization, Simultaneous Equations
In algebra, factoring is a technique to simplify an expression by reversing the multiplication process. Simultaneous Equations are a set of two or more algebraic equations that share variables and are solved simultaneously. In this chapter, we will learn about factoring by grouping, review the three steps, explore splitting the middle term, and work examples to practice verification and what simultaneous equations are with examples. Find out how to solve the equations using the methods of elimination, graphing, and substitution.
0/10
Algebraic Formulas
06:35
Stimulation – Area Model Algebra
00:00
Factorization
00:00
Manipulation of Algebraic Expression
00:00
Stimulation – Equality Explorer
00:00
Linear Equations in One Variable
00:00
Simultaneous Linear Equations
00:00
Stimulation – Equality Explorer (Two Variables)
00:00
Elimination
00:00
Let's Try
Chapter 07 – Fundamentals of Geometry
Geometry is the study of different types of shapes, figures, and sizes. It is important to know and understand some basic concepts. We will learn about some of the most fundamental concepts in geometry, including lines, polygons, and circles.
0/4
Parallel Lines
05:35
Polygons
04:11
Circles
03:14
Let's Try
Chapter 08 – Practical Geometry
Geometric construction offers the ability to create accurate drawings and models without the use of numbers. In this chapter, we will discover the methods and tools that will aid in solving math problems as well as constructing quadrilaterals and right-angled triangles.
0/3
Construction of Quadrilaterals
11:16
Construction of a Right Angled Triangle
07:38
Let's Try
Chapter 09 – Areas and Volumes
The volume and surface area of a sphere can be calculated when the sphere's radius is given. In this chapter, we will learn about the shape sphere and its radius, and understand how to calculate the volume and surface area of a sphere through some practice problems. Also, we will learn to use and apply Pythagoras' theorem and Herons' formula.
0/7
Pythagoras Theorem
00:00
Let's Try
Math Lab
Heron’s Formula
04:42
Let's Try
Surface Area, and Volume of a Sphere
03:20
Let's Try
Chapter 10 – Demonstrative Geometry
Demonstrative geometry is a branch of mathematics that is used to demonstrate the truth of mathematical statements concerning geometric figures. In this chapter, we will learn about theorems on geometry that are proved through logical reasoning.
0/5
Reasoning
03:34
Axioms
00:00
Postulate
05:01
Theorems
00:00
Let's Try
Chapter 11 – Trigonometry
Sine and cosine are basic trigonometric functions used to solve the angles and sides of triangles. In this chapter, we will review trigonometry concepts and learn about the mnemonic used for sine, cosine, and tangent functions.
0/7
What is Trigonometry?
00:00
Visualization of Trigonometric Ratios
02:55
Let's Try
Trigonometric Ratios of Complementary Angles
05:21
Simulation – Trig Tour
00:00
Angle of Elevation and Angle of Depression
04:22
Let's Try
Chapter 12 – Information Handling
Frequency distribution, in statistics, is a graph or data set organized to show the frequency of occurrence of each possible outcome of a repeatable event observed many times. Measures of central tendency describe how data sets are clustered in a central value. In this chapter, we will learn to construct the frequency distribution table, and learn more about three measures of central tendency, its importance, and various examples.
0/9
Frequency Distribition
01:03
Let's Try
Bar Graph
07:49
Histogram
00:00
Pie Chart
04:29
Let's Try
Measures of Central Tendency
00:00
Mean, Median, and Mode
03:17
Let's Try
Mathematics – VIII
About Lesson

In all triangles, the sum of the measures of all angles must be <span id="MathJax-Element-1-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="180∘.” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>180∘. Since a right angle has a measure of <span id="MathJax-Element-2-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="90∘,” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>90∘, the remaining two angles in a right-angled triangle must be complementary. 

Trigonometric Ratio of Complementary Angles

” Two angles whose sum is <span id="MathJax-Element-1-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="90∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>90∘ are called complementary angles.”

Two angles are said to be complementary if their sum is <span id="MathJax-Element-3-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="90∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>90∘. It follows from the above definition that <span id="MathJax-Element-4-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="θ” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>θ and <span id="MathJax-Element-5-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="(90∘−θ)” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>(90∘−θ) are complementary angles for an acute angle <span id="MathJax-Element-6-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="θ” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>θ. Recall that the sine and cosine of angles are ratios of pairs of sides in right-angled triangles.

  • The sine of an angle in a right-angled triangle is the ratio of the side opposite the angle to the hypotenuse.
  • The cosine of an angle in a right-angled triangle is the ratio of the side adjacent to the angle to the hypotenuse.

In a right-angled triangle, <span id="MathJax-Element-7-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="PQR” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>ABC, right-angled at <span id="MathJax-Element-8-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="Q” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>B, the sum of the measures of the three angles in a triangle is <span id="MathJax-Element-9-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="180∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>180∘. This means that <span id="MathJax-Element-10-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="m∠P+m∠Q+m∠R=180∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>m∠A + m∠B + m∠C = 180∘. <span id="MathJax-Element-11-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="∠Q” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>∠B is a right angle so <span id="MathJax-Element-12-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="m∠Q=90∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>m∠B = 90∘. Therefore, <span id="MathJax-Element-13-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="m∠P+m∠R=90∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>m∠A + m∠C = 90∘. Since the measures of these acute angles add to <span id="MathJax-Element-14-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="90∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>90∘, we know these acute angles are complementary.

Trigonometric Ratios for Complementary Angles

  • The sine of any acute angle is equal to the cosine of its complement and vice versa.
  • The <span class="x-ck12-vocab-interlink" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font: inherit; vertical-align: baseline; color: var(–link-base-color); text-decoration: none; cursor: pointer;" role="term" data-equation_latex="\cot{\theta}=\frac{1}{\tan{\theta}}” data-plural=”” data-definition=”The%20cotangent%20of%20an%20angle%20in%20a%20right%20triangle%20is%20a%20relationship%20found%20by%20dividing%20the%20length%20of%20the%20side%20adjacent%20to%20the%20given%20angle%20by%20the%20length%20of%20the%20side%20opposite%20to%20the%20given%20angle.%20If%20the%20hypotenuse%20is%20of%20unit%20length%2C%20the%20cotangent%20is%20the%20reciprocal%20of%20the%20tangent%20function%20or%20%3Cmath%3E%5Ccot%7B%5Ctheta%7D%3D%5Cfrac%7B1%7D%7B%5Ctan%7B%5Ctheta%7D%7D%3C/math%3E.” data-id=”13614″ data-languageid=”1″ data-term=”Cotangent” data-json=”eyJkYXRhLWVxdWF0aW9uX2xhdGV4IjogIjxtYXRoPlxcY290e1xcdGhldGF9PVxcZnJhY3sxfXtcXHRhbntcXHRoZXRhfX08L21hdGg+IiwgImRhdGEtcGx1cmFsIjogIiIsICJkYXRhLWRlZmluaXRpb24iOiAiVGhlJTIwY290YW5nZW50JTIwb2YlMjBhbiUyMGFuZ2xlJTIwaW4lMjBhJTIwcmlnaHQlMjB0cmlhbmdsZSUyMGlzJTIwYSUyMHJlbGF0aW9uc2hpcCUyMGZvdW5kJTIwYnklMjBkaXZpZGluZyUyMHRoZSUyMGxlbmd0aCUyMG9mJTIwdGhlJTIwc2lkZSUyMGFkamFjZW50JTIwdG8lMjB0aGUlMjBnaXZlbiUyMGFuZ2xlJTIwYnklMjB0aGUlMjBsZW5ndGglMjBvZiUyMHRoZSUyMHNpZGUlMjBvcHBvc2l0ZSUyMHRvJTIwdGhlJTIwZ2l2ZW4lMjBhbmdsZS4lMjBJZiUyMHRoZSUyMGh5cG90ZW51c2UlMjBpcyUyMG9mJTIwdW5pdCUyMGxlbmd0aCUyQyUyMHRoZSUyMGNvdGFuZ2VudCUyMGlzJTIwdGhlJTIwcmVjaXByb2NhbCUyMG9mJTIwdGhlJTIwdGFuZ2VudCUyMGZ1bmN0aW9uJTIwb3IlMjAlM0NtYXRoJTNFJTVDY290JTdCJTVDdGhldGElN0QlM0QlNUNmcmFjJTdCMSU3RCU3QiU1Q3RhbiU3QiU1Q3RoZXRhJTdEJTdEJTNDL21hdGglM0UuIiwgImRhdGEtaWQiOiAxMzYxNCwgImRhdGEtbGFuZ3VhZ2VJRCI6IDEsICJkYXRhLXRlcm0iOiAiQ290YW5nZW50In0=” data-interlink-id=”x-ck12-9m6vhoirvanecytp” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font: inherit; vertical-align: baseline; color: var(–link-base-color); text-decoration: none; cursor: pointer;” data-mce-tabindex=”0″>cotangent of any acute angle is equal to the tangent of its complement and vice versa.
  • The <span class="x-ck12-vocab-interlink" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font: inherit; vertical-align: baseline; color: var(–link-base-color); text-decoration: none; cursor: pointer;" role="term" data-equation_latex="\csc{\theta}=\frac{1}{\sin{\theta}}” data-plural=”” data-definition=”The%20cosecant%20of%20an%20angle%20in%20a%20right%20triangle%20is%20a%20relationship%20found%20by%20dividing%20the%20length%20of%20the%20hypotenuse%20by%20the%20length%20of%20the%20side%20opposite%20to%20the%20given%20angle.%20If%20the%20hypotenuse%20is%20of%20unit%20length%2C%20the%20cosecant%20is%20the%20reciprocal%20of%20the%20sine%20function%20or%20%3Cmath%3E%5Ccsc%7B%5Ctheta%7D%3D%5Cfrac%7B1%7D%7B%5Csin%7B%5Ctheta%7D%7D%3C/math%3E.” data-id=”13610″ data-languageid=”1″ data-term=”Cosecant” data-json=”eyJkYXRhLWVxdWF0aW9uX2xhdGV4IjogIjxtYXRoPlxcY3Nje1xcdGhldGF9PVxcZnJhY3sxfXtcXHNpbntcXHRoZXRhfX08L21hdGg+IiwgImRhdGEtcGx1cmFsIjogIiIsICJkYXRhLWRlZmluaXRpb24iOiAiVGhlJTIwY29zZWNhbnQlMjBvZiUyMGFuJTIwYW5nbGUlMjBpbiUyMGElMjByaWdodCUyMHRyaWFuZ2xlJTIwaXMlMjBhJTIwcmVsYXRpb25zaGlwJTIwZm91bmQlMjBieSUyMGRpdmlkaW5nJTIwdGhlJTIwbGVuZ3RoJTIwb2YlMjB0aGUlMjBoeXBvdGVudXNlJTIwYnklMjB0aGUlMjBsZW5ndGglMjBvZiUyMHRoZSUyMHNpZGUlMjBvcHBvc2l0ZSUyMHRvJTIwdGhlJTIwZ2l2ZW4lMjBhbmdsZS4lMjBJZiUyMHRoZSUyMGh5cG90ZW51c2UlMjBpcyUyMG9mJTIwdW5pdCUyMGxlbmd0aCUyQyUyMHRoZSUyMGNvc2VjYW50JTIwaXMlMjB0aGUlMjByZWNpcHJvY2FsJTIwb2YlMjB0aGUlMjBzaW5lJTIwZnVuY3Rpb24lMjBvciUyMCUzQ21hdGglM0UlNUNjc2MlN0IlNUN0aGV0YSU3RCUzRCU1Q2ZyYWMlN0IxJTdEJTdCJTVDc2luJTdCJTVDdGhldGElN0QlN0QlM0MvbWF0aCUzRS4iLCAiZGF0YS1pZCI6IDEzNjEwLCAiZGF0YS1sYW5ndWFnZUlEIjogMSwgImRhdGEtdGVybSI6ICJDb3NlY2FudCJ9″ data-interlink-id=”x-ck12-gbk2ga3j3yxm0rq4″ data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font: inherit; vertical-align: baseline; color: var(–link-base-color); text-decoration: none; cursor: pointer;” data-mce-tabindex=”0″>cosecant of any acute angle is equal to the secant of its complement and vice versa. 

Example:

If <span id="MathJax-Element-53-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="sin⁡30∘=12, cos?=12″ data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>sin⁡30∘ = 1/2, cos ? = 1/2.

The sine and cosine of complementary angles are equal. 

<span id="MathJax-Element-54-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="90∘−30∘=60∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>90∘ − 30∘ = 60∘  is complementary to <span id="MathJax-Element-55-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="30∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>30∘.

Therefore, <span id="MathJax-Element-56-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="cos⁡60∘=12″ data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>cos⁡60∘=1/2.

Example:

Consider the right-angled triangle below. Find <span id="MathJax-Element-57-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡A” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡A and <span id="MathJax-Element-58-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡B” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡B.

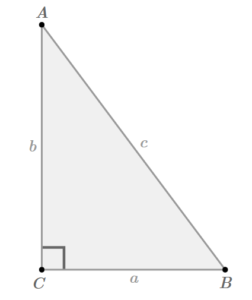
<span id="MathJax-Element-59-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡A=BCAC=ab” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡A=BC/AC=a/b and <span id="MathJax-Element-60-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡B=ACBC=ba” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡B=AC/BC=b/a.

The tangent of any angle is opposite over adjacent so <span id="MathJax-Element-61-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡B=ACBC” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡B=AC/BC and <span id="MathJax-Element-62-Frame" class="MathJax_SVG" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;" role="presentation" data-mathml="tan⁡A=BCAC” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; font-style: normal; font-variant: inherit; font-weight: normal; font-stretch: inherit; font-size: 18px; line-height: normal; font-family: inherit; vertical-align: baseline; display: inline-block; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; outline: none; position: relative;” data-mce-tabindex=”0″>tan⁡A=BC/AC. These are inverses of each other, therefore the tangents of complementary angles are inverses of each other.

Example:

Given the trigonometric ratios of <span id="MathJax-Element-39-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="30∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>30∘, find all the six trigonometric ratios of <span id="MathJax-Element-40-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="60∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>60∘

Solution: 

Since <span id="MathJax-Element-53-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="30∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>30∘ and <span id="MathJax-Element-54-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="60∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>60∘ are complementary angles, we can use the method of co-ratios to determine trigonometric ratios of  <span id="MathJax-Element-55-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="60∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>60∘ using those of <span id="MathJax-Element-56-Frame" class="MathJax" style="box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;" role="presentation" data-mathml="30∘” data-mce-style=”box-sizing: border-box; margin: 0px; padding: 0px; border: 0px; vertical-align: baseline; display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 15px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; position: relative;” data-mce-tabindex=”0″>30∘ as shown below:

Previous
Next
0% Complete